今日の一問 数学(広島県・改)
2014/03/11
-相似の問題-
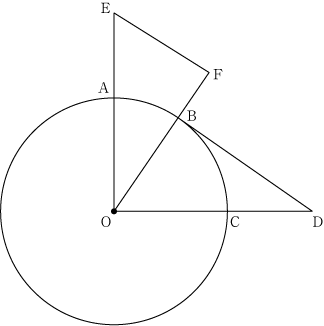
下の図のように、円Oの円周上に3点A,B,Cがあり、∠AOC=90°です。点Bにおける円Oの接線と線分OCの延長との交点をDとします。線分OAの延長上にEO=ODとなるように点Eをとります。点Eから直線OBに垂線をひき、直線OBとの交点をFとします。
このとき、EF=OBであることを証明しなさい。
<答え>
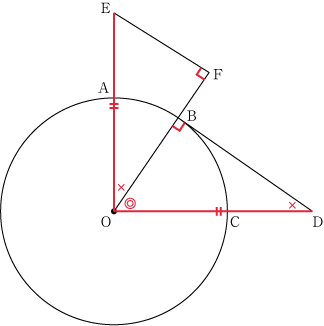
△EOFと△ODBにおいて
EO = OD ・・・①
∠EFO = 90° ・・・②
BDは円Oの接線であるから
∠OBD = 90° ・・・③
∠AOC = 90°であるから
∠EOF + ∠BOD = 90° ・・・④
また、③より
∠ODB + ∠BOD = 90° ・・・⑤
④,⑤より、∠EOF = ∠ODB ・・・⑥
①,②,③,⑥より、直角三角形の斜辺と1つの鋭角がそれぞれ等しいから
△EOF ≡ △ODB
したがって、EF = OB
<ワンポイントアドバイス>
直角三角形の合同条件は以下の2パターン。どちらも条件に斜辺が含まれることがポイントなので、2つとも必ず覚えておこう。
・直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
・直角三角形の斜辺と他の1辺がそれぞれ等しい。
