今日の一問 数学(千葉県・改)
2013/10/01
-確率の問題-
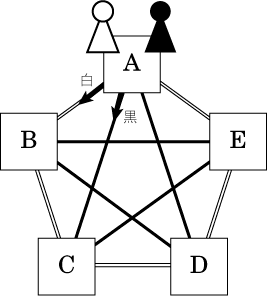
下の図のように、A~Eの5つのマス目を進む白いコマと黒いコマがAのマス目に置いてある。
大小2つのサイコロを同時に1回投げ、大きいサイコロの出た目の数だけ、白いコマをAから1マスずつB→C→D→E→A→Bの順に進ませ、小さいサイコロの出た目の数だけ、黒いコマをAから1マスずつC→E→B→D→A→Cの順に進ませる。
このとき、白いコマと黒いコマが同じマス目に止まる確率を求めなさい。
ただし、サイコロを投げるとき、1から6までのどの目が出ることも同様に確からしいものとする。
<答え>
36分の7
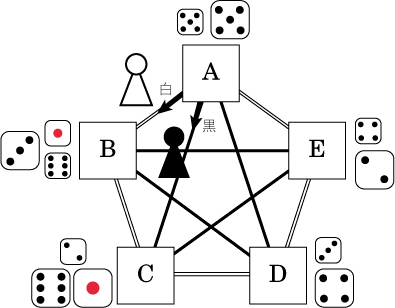
下の図のように、同じマス目に止まるサイコロの組み合わせは7通り。
(大,小)=(1,2)(2,4)(3,1)(3,6)(4,3)(5,5)(6,2)
<ワンポイントアドバイス>
大小2つのサイコロを使った問題ですが、本問のように少しひねった形の出題も考えられます。
その場合、とりあえず問題文に書いてある通りにサイコロの数字を書き加えてみよう。
必ず条件に合致する組み合わせを見つけることができるので、そこから確率を求めることができます。