今日の一問 数学(福岡県・改)
2013/07/30
-角の問題-
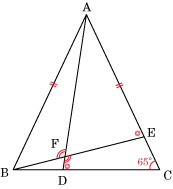
下の図のように、AB = AC,∠BAC = 50°の二等辺三角形ABCがある。
辺BC,AC上にそれぞれ点D,Eをとり、線分AD,BEの交点をFとする。
∠ADC = ∠AEBのとき、∠AFBの大きさは何度になるか。
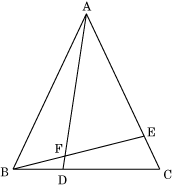
<答え>
115°
△ABCは二等辺三角形なので、∠BAC = 50°より∠BCA = 65°になる。
四角形FDCEの内角の和は360°なので、∠EFD + ∠FDC + ∠DCA + ∠CEF = 360°
したがって、∠EFD = 360° - (∠FDC + ∠DCE + ∠CEF)
∠CEF = 180° - ∠AEB より
∠EFD = 360° - (∠FDC + 65° + (180° - ∠AEB))
∠AEB = ∠FDC より
∠EFD = 360° - (∠FDC + 65° + (180° - ∠FDC))
∠EFD = 360° - ( 65° + 180°) = 115°
対頂角のため ∠AFB = ∠EFD = 115°
<ワンポイントアドバイス>
問題文の条件の中に∠ADC = ∠AEBとあるため、この2つの角を外角と内角に利用するとうまく消えてくれる。
また、以下のように△BCEを利用して求める方法もある。
外角∠AEB = ∠EBC + 65° なので、∠ADC = ∠AEB より ∠ADC = ∠EBC + 65°
したがって、∠BFD = 65°になり、∠AFB = 115° になる。