今日の一問 数学(大阪府・改)
-空間図形の問題-
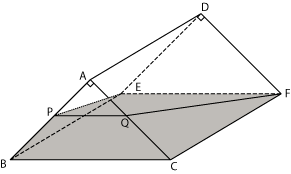
下の図において立体ABC-DEFは三角柱である。△ABCと△DEFは合同な直角二等辺三角形であり、∠BAC=∠EDF=90°である。
四角形ACFD,ABED,BCFEはすべて長方形であり、AD=10cm、AB=AC=8cmとする。
P,Qはそれぞれ辺AB,AC上にあって、AP=AQとなる点である。
PとE、PとQ、QとFをそれぞれ結ぶ。このとき、4点P,Q,F,Eは同じ平面上にあって、QF=11cmである。
1.線分PQの長さを求めなさい。求め方も書くこと。
2.立体PQ-BCFEの体積を求めなさい。
<答え>

<ワンポイントアドバイス>
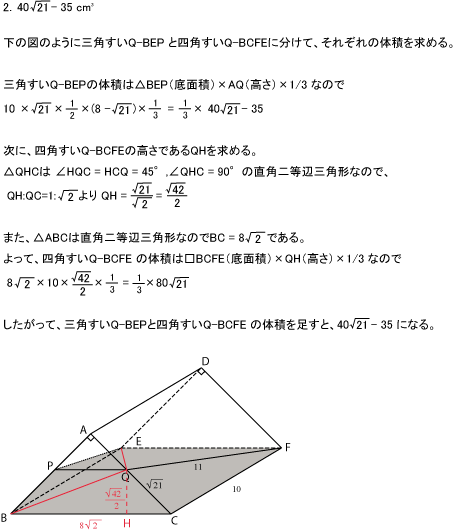
まず、そのままの形では体積を求めることができないことが分かるはず。
したがって、角すいや角柱に分けて、それぞれの体積を求めることで、全体の体積を求めることになる。
今回は角すいを2つ作ることで答えを求めましたが、角柱と角すいに分けることもできるので、あとで自分で試してみよう。