今日の一問 数学(長野県・改)
2013/08/27
-相似な図形の問題-
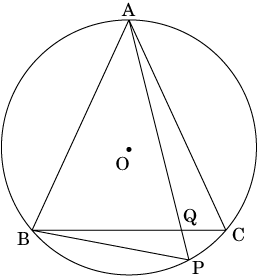
AB = AC である二等辺三角形ABC が円Oに内接している。下の図のように、円周上の点A,B,C とは異なる位置に点Pをとり、点AとP、 点BとPを直線で結び、直線APと直線BCの交点をQとする。
①△ABP ∽ △AQB を証明しなさい。
②AB = 10cm、AQ:QP = 9:1 のとき、線分AQの長さを求めなさい。
<答え>
①
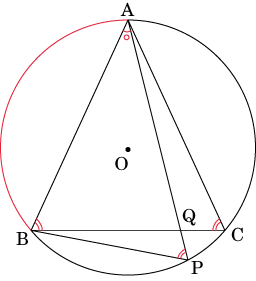
△ABPと△AQBにおいて
弧ABに対する円周角は等しいので、
∠APB = ∠ACB ・・・①
二等辺三角形ABCの底角は等しいので、
∠ACB = ∠ABQ ・・・②
①と②より ∠APB = ∠ABQ ・・・③
また、∠BAP = ∠QAB ・・・④
③と④より、2組の角がそれぞれ等しいので、
△ABP ∽ △AQB
②
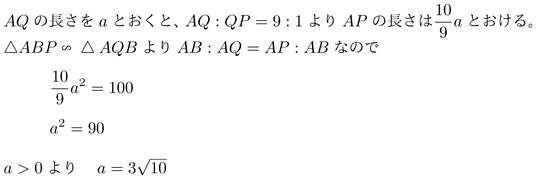
<ワンポイントアドバイス>
線分の長さを求める問題において、比の値が与えられている場合は、必ず相似な図形を利用することになります。
本文のように、①で相似を証明させて、それを利用して②を答えさせるパターンが多いので、長さを求める線分に対応する線分を見つけることができれば、あとは計算するだけで答えを導くことができます。
