今日の一問 数学(岡山県・改)
2013/08/19
-合同証明の問題-
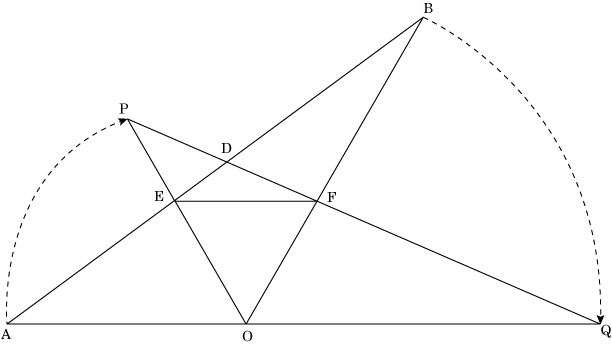
下の図のように、△OABと△OPQがあり、△OAB ≡ △OPQ、∠AOB = 120° である。
△OABを点Oを回転の中心として、時計の針の回転と同じ向き(矢印の方向)に60°回転移動させると、△OPQとちょうど重なる。
線分ABと線分PQとの交点をD、線分ABと線分POとの交点をE、線分OBと線分PQとの交点をFとし、点Eと点Fを結ぶ。
このとき、△OBE ≡ △OQFを証明しなさい。
<答え>
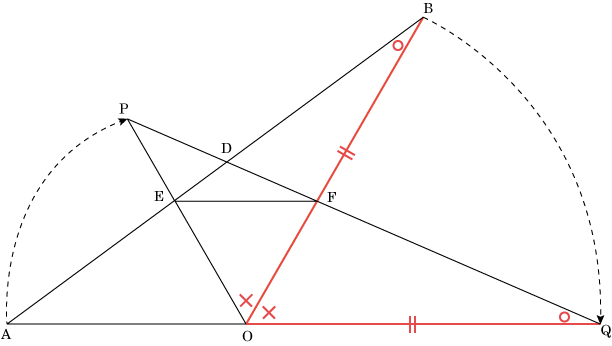
△OBEと△OQFにおいて、△OAB ≡ △OPQだから、
OB = OQ ・・・①
∠EBO = ∠FQO ・・・②
△OABを点Oを回転の中心として60°回転移動させると、△OPQに重なることから、
∠EOB = ∠AOB - ∠AOE = 120° - 60° = 60° ・・・③
∠FOQ = 60° ・・・④
③④から、∠EOB = ∠FOQ ・・・⑤
①②⑤から、1辺とその両端の角がそれぞれ等しいので、△OBE ≡ △OQF である。
<ワンポイントアドバイス>
三角形の合同の条件は、以下の3つがあります。
①3組の辺がそれぞれ等しい
②2組の辺とその間の角がそれぞれ等しい
③1組の辺とその両端の角がそれぞれ等しい
いずれの条件にも辺の条件が含まれているので、まず等しい辺を見つけることから始めよう。
次に、等しくなる角を見つけることができれば、それらの角と辺を組み合わせて証明することができます。
