今日の一問 数学(愛媛県・改)
2014/02/25
-確率の問題-
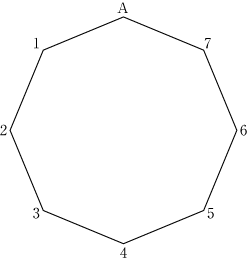
下の図のような正八角形があり、1つの頂点にはAが、他の7つの頂点には、1から7までの番号がふられている。
1から7までの数字が1つずつ書かれた7枚のカードから2枚のカードを取り出し、カードに書かれた数字と同じ番号の2点と、点Aの3点を結んで、これらの3点を頂点とする三角形をつくる。このとき、その三角形が直角三角形となる確率を求めよ。ただし、どのカードが取り出されることも同様に確からしいものとする。
<答え>
7分の3
点Aを含む3点を結んで三角形を作るには、残りの1~7の頂点の中から2点を選べばよいので、7枚のカードから2枚のカードを選ぶときの組み合わせを考えると、全部で21通り(7×6÷2=21 ※注:「1・2」のペアは「2・1」と同じなので2で割る)になる。
次に、直角三角形の組合せを考える。正多角形は円に内接するので、円の直径と円周角との関係から、以下の9つの組み合わせが直角三角形になることが分かる。(5~7の頂点は重複する(例:5→1は1→5と同じこと)ので無視できる。)

<ワンポイントアドバイス>
まず、すべての組み合わせ(直角三角形を含むあらゆる三角形になる組み合わせ)の数を求めることができなければ何も始まらないので、基本的な考え方をしっかり理解しておこう。
3つの頂点のうち、Aを1つ目の頂点と考えると、A以外の7つの頂点から2つ目に選べる頂点は7つあって、残った6つの頂点から3つ目に選べる頂点は6つあるので、7通り×6通り=42通りという考え方をします。このまま重複する組み合わせを考えなければ、直角三角形になる組み合わせは18(上の図の2倍)あるので、求める確率は18÷42=3/7で同じ確率になります。
