今日の一問 数学(三重県・改)
2014/02/11
-空間図形の問題-
右の図のように、立方体の4つの頂点A、B、C、Dを結んでできる立体Kがある。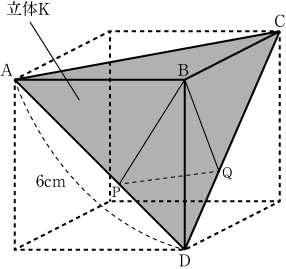
辺AD上に点Pを、辺CD上に点Qをそれぞれとり、3つの線分BP、PQ、QBの長さの和が最小となるようにする。
このとき、3つの線分の長さの和を求めなさい。
ただし、辺ADの長さは6cmとする。
<答え>
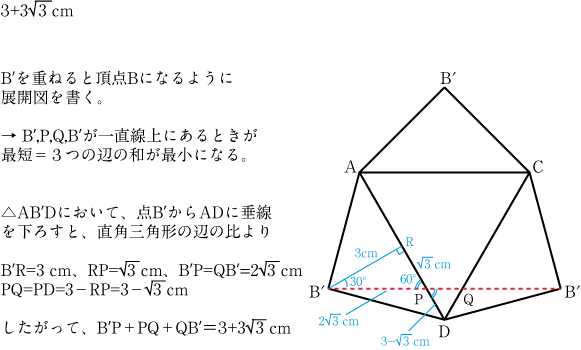
<ワンポイントアドバイス>
“辺の和が最小になるとき”という出題パターンはよくあります。
本問のように、空間図形の場合は、展開図を丁寧に書くことがポイントになります。適当に書いてしまうと辺と角の位置関係が曖昧になってしまうからです。
あとは、設問の対象となる辺が一直線になるように補助線を引くことができれば、正解にたどり着けるはずです。
