今日の一問 数学(広島県・改)
2013/11/05
-図形の問題-
下の図のように、△ABCの辺BC上に点Dがあり、AD=AC、∠CAD=2∠BADである。
AB=15cm、CD=8cmのとき、△ABDの面積は何cm²ですか。
<答え>
30cm²
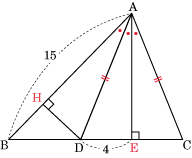
線分CDの中点をE、点Dから辺ABに垂線DHをひく。
このとき、△ADEと△ADHにおいて、
仮定より、
∠DAH=∠DAE(二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する)
∠AED=∠AHD=90°
ADは共通な辺より、直角三角形の斜辺と1つの鋭角がそれぞれ等しいから、△ADE≡△ADH
したがって、DH=DE=CE=4cm
△ABDの面積は、15×4×½=30(cm²)になる。
<ワンポイントアドバイス>
補助線をうまく引けるかどうかがポイントになる問題です。
本問の場合、問題文に∠CAD=2∠BADとあるので、とりあえず、点Aから辺BCに垂線を引いてみる。また、△ABDの面積が問われていることから、底辺をABと考えると高さが分かればよいので、点Dから辺ABに垂線を引いてみる。こうして出来上がった図形を手がかりにして考えていくと、なんとなく方針が見えてくるはずなので、取っ掛かりが見えない問題が出た場合、とにかく補助線を引いてみることから始めてみよう。
